210 children tickets are sold
Solution:
Let "x" be the number of child tickets sold
Let "y" be the number of adult tickets sold
Cost of 1 adult ticket = $ 7
Cost of 1 child ticket = $ 3
Given that 370 people bought tickets to a fair
number of child tickets sold + number of adult tickets sold = 370
x + y = 370 ------ eqn 1
Total revenue was $1750. Therefore,
number of child tickets sold x Cost of 1 child ticket + number of adult tickets sold x Cost of 1 child ticket = 1750
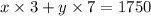
3x + 7y = 1750 ------ eqn 2
Let us solve eqn 1 and eqn 2
From eqn 1,
x = 370 - y ------- eqn 3
Substitute eqn 3 in eqn 2
3(370 - y) + 7y = 1750
1110 - 3y + 7y = 1750
4y = 1750 - 1110
4y = 640
y = 160
From eqn 3,
x = 370 - 160
x = 210
Thus 210 children tickets are sold