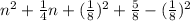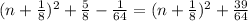Answer:
1)
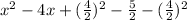
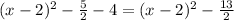
2)
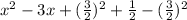
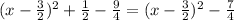
3)
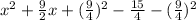
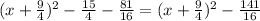
4)
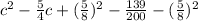
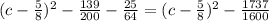
5)
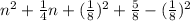
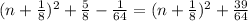
Explanation:
1. −2x^2 + 8x + 5
For this case we can begin dividing all the terms by -2 and we got:
![x^2 -4x -(5)/(2)[/tex</p><p>And if we complete the square we got:</p><p>[tex] x^2 -4x +((4)/(2))^2 -(5)/(2) - ((4)/(2))^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/k5rcxruu7hlcputbsd6x7pgptvj9dmyty2.png)
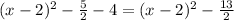
2. 2.5x^2 − 7.5x + 1.25
For this case we can begin dividing all the terms by 2.5 and we got:
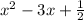
And if we complete the square we got:
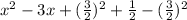
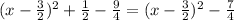
3. 4 / 3x ^2 + 6x − 5
For this case we can begin dividing all the terms by 4/3 and we got:
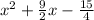
And if we complete the square we got:
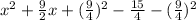
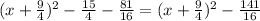
4. 1000c^2 − 1250c + 695
For this case we can begin dividing all the terms by 1000 and we got:
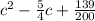
And if we complete the square we got:
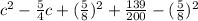
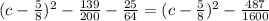
5. 8n^2 + 2n + 5
For this case we can begin dividing all the terms by 8 and we got:
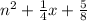
And if we complete the square we got: