Question

The final exam scores in freshman English at a large high school are normally distributed with a mean of 84% and a standard deviation of 14. If 450 students took the exam, approximately how many students scored between 70% and 80%? (please show work)

A. 103
B. 125
C. .2289
D. 99
E. 95

Answer 1

Answer: A. 103

Explanation:

Given : The final exam scores in freshman English at a large high school are normally distributed with a mean of 84% and a standard deviation of 14%.

i.e.
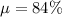`\mu=84\%` and
`\sigma=14\%`

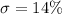
Let x be the exam scores in freshman English ( in percent ).

Then, the probability that students scored between 70% and 80% would be

`P(70<x<80) =P((70-84)/(14)<(x-\mu)/(\sigma)<(80-84)/(14))\\\\=P(-1<z<-0.2875)\ \ [\beacuse \ z=(x-\mu)/(\sigma)]\\\\=P(z<-0.2875)-P(z<-1)\\\\=(1-P(z<0.2875))-(1-P(x<1))\ \ [\because P(Z<-z)=1-P(Z<z)]\\\\=P(z<1)-P(z<0.2875)\\\\= 0.8413-0.6124=0.2289\ \ [\text{By z-table}]`

If 450 students took the exam, then the number of students scored between 70% and 80% = 450 x ( probability that students scored between 70% and 80%)

= 450 x 0.2289=103.005≈ 103

Therefore , About 103 students scored between 70% and 80% .

Hence, the correct answer is A. 103 .