Answer:
Factoring
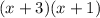
Completing the square
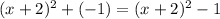
For this case seems more complicated the option completing the square because we need to do more operations and we need to know algebra. By the other hand for the Factoring case we just need to find two numbers that satisfy the conditions required.
Explanation:
Assuming the following expression:
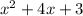
Factoring
For this case we want to find two values that added would be 4 and multiplied would be 3. On this case these two values are 3 and 1 because 3+1=4 and 3*1 =3. So then we can factor the expression like this:
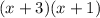
Completing the square
For this case if we want to complete the square we need to do this:
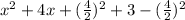
And if we simplify this we got:
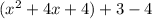
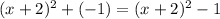
For this case seems more complicated the option completing the square because we need to do more operations and we need to know algebra. By the other hand for the Factoring case we just need to find two numbers that satisfy the conditions required.