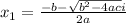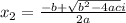Question

Solve ax^2 + ????x + c = 0.

Answer 1

See solution and explanation below.

Explanation:

Assuming that on this case our equation is this one:

`ax^2 + bx + c=0`

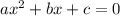
We can use the quadratic formula in order to solve this problem. And the quadratic formula is given by:

`x= (-b \pm √(b^2 -4ac))/(2a)`

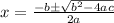
If the discriminant is >0
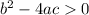`b^2 -4ac >0` we have two real solutions

And the possible two solutions are:

`x_1= (-b - √(b^2 -4ac))/(2a)`

`x_2= (-b + √(b^2 -4ac))/(2a)`

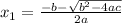
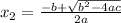
If the discriminant is equal to 0.
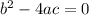`b^2 -4ac =0` we have just one real solution:

`x = (-b)/(2a)`

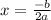
If the discriminant is lower than 0.
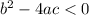`b^2 -4ac <0` we have two imaginaty solutions.

`x_1= (-b - √(b^2 -4ac)i)/(2a)`

`x_2= (-b + √(b^2 -4ac)i)/(2a)`