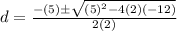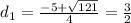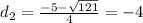Answer:
5)

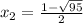
6)
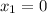
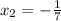
7) So for this case we have just one solution
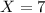
8)
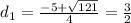
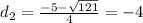
Explanation:
5. x^2 − 1x + 19 = −5
For this case we can rewrite the expression like this:

And then we can use the quadratic formula given by:
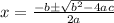
And for this case a= 1, b = -1 , c = 24, and replacing we got:
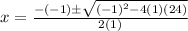

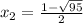
6. 7x^2 + x = 0
For this case we can take common factor first like this:
[tex x (7x +1) = 0[/tex]
So then
 or
or
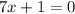 and we got that:
and we got that:
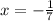
7. 7x^2 − 14x = −7
We can rewrite the expression like this:
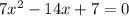
And then we can use the quadratic formula given by:
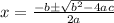
And for this case a= 7, b = -14 , c = 7, and replacing we got:
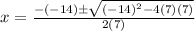
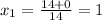
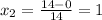
So for this case we have just one solution
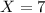
8. 2d^2 + 5d − 12 = 0
We can use the quadratic formula given by:
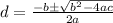
And for this case a= 2, b = 5 , c = -12, and replacing we got: