Square the following general examples to determine the general rule for squaring a binomial: a. (a + ????)^2 b. (a − ????)^2

Question

asked Sep 8, 2021 176k views

1 Answer

Magnus Akselvoll · Answer 1 · 2021-09-13T20:07:26+0000

Answer:

See explanation below.

Explanation:

For part a we have the following expression:

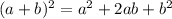
(a+b)^2 = a^2 +2ab + b^2

And for part b we got:

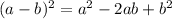
(a-b)^2 = a^2 -2ab +b^2

On general we have the following formula:

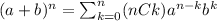
$(a+b)^n =\sum_(k=0)^n (nCk) a^(n-k) b^k$

We see that if n=2 we have this:

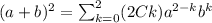
$(a+b)^2 =\sum_(k=0)^2 (2Ck) a^(2-k) b^k$

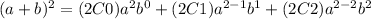
(a+b)^2 = (2C0) a^2 b^0 + (2C1)a^(2-1) b^1 + (2C2) a^(2-2) b^2

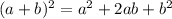
(a+b)^2 = a^2 +2ab + b^2

And for the other possibility we have:

$(a+b)^n =\sum_(k=0)^n (-1)^k (nCk) a^(n-k) b^k$

We see that if n=2 we have this:

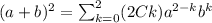
$(a+b)^2 =\sum_(k=0)^2 (2Ck) a^(2-k) b^k$

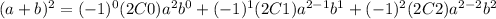
(a+b)^2 = (-1)^0 (2C0) a^2 b^0 +(-1)^1 (2C1)a^(2-1) b^1 + (-1)^2 (2C2) a^(2-2) b^2

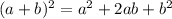
(a+b)^2 = a^2 +2ab + b^2

So then we have the general expression for any binomial term elevated at any power.