Question

The x-values below are hours spent studying, and the y-values are grades on a test. What is the Pearson product-moment correlation coefficient? x = {3.2, 3, 1, 2.5, 1.9} y = {90, 88, 57, 86, 79}

Answer 1

The Pearson product-moment correlation coefficient is
`r = 0.9556`

Explanation:

The Pearson product-moment correlation coefficient (PMCC) is a numerical value between -1 and 1 that expresses the strength of the linear relationship between two variables.When r is closer to 1 it indicates a strong positive relationship. A value of 0 indicates that there is no relationship. Values close to -1 signal a strong negative relationship between the two variables.

To find the PMCC of the following data, you must:

`\begin{array}cX&3.2&3&1&2.5&1.9\\Y&90&88&57&86&79\end{array}`

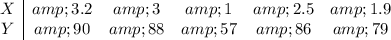
Step 1: Find
`X\cdot Y`,
`X\cdot X` and
`Y\cdot Y` as it was done in the table below.

Step 2: Find the sum of every column to get

`\sum{X}=11.6 ~,~ \sum{Y}=400 ~,~ \sum{X \cdot Y}=974.1 ~,~ \sum{X^2}=30.1  ~,~ \sum{Y^2}=32730`

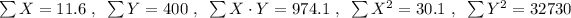
Step 3: Use the following formula to find the PMCC.

`\begin{aligned}r~&=~\frac{n\cdot\sum{XY} - \sum{X}\cdot\sum{Y}}         {\sqrt{\left[n \sum{X^2}-\left(\sum{X}\right)^2\right] \cdot \left[n \sum{Y^2}-\left(\sum{Y}\right)^2\right]}} \\r~&=~\frac{ 5 \cdot 974.1 - 11.6 \cdot 400 }         {√(\left[ 5 \cdot 30.1 - 11.6^2 \right] \cdot \left[ 5 \cdot 32730 - 400^2 \right] )} \approx 0.9556\end{aligned}`