Question

The tennis team has a robot that picks up tennis balls. The tennis court is 36 feet wide and 78 feet long. The robot

starts at position (8,10) and is at position (16,20) at t = 4 seconds after moving at a constant speed. When will it
pick up the ball located at position (28,35)?

Answer 1

`t = t_1 +t_2 = 4 sec+6 sec = 10 sec`

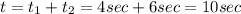
Explanation:

Let's call the initial point
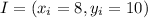`I= (x_i=8,y_i=10)` and the second point
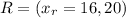`R=(x_r = 16, 20)` we can find the distance between these two points with the following formula:

`d_1 = √((x_r -x_i)^2 +(y_r -y_i)^2)`

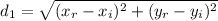
And if we replace we got:

`d_1 = √((16 -8)^2 +(20 -10)^2) =2√(41)`

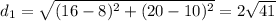
So since we know the time in order to reach the point R we can find the velocity like this:

`v=(d_1)/(t_1) = (2√(41))/(4)=(√(41))/(2)`

And this velocity is constant along all the displacement.

Let's call the final point
`F =(x_f = 28, y_f = 35)`

And we can find the distance between the point R and F
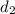`d_2` like this:

`d_2 = √((x_f -x_r)^2 +(y_f -y_r)^2)`

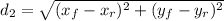
And if we replace we got:

`d_2 = √((28 -16)^2 +(35 -20)^2)=3√(41)`

Since the velocity is constant we can find the time between point R and F like this:

`t_2 = (3√(41))/((√(41))/(2))=6 sec`

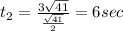
And we are interested on "When will it pick up the ball located at position (28,35)?" And then the total time would be:

`t = t_1 +t_2 = 4 sec+6 sec = 10 sec`

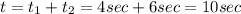
The figure attached illustrate the problem.