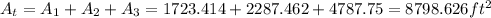Answer:
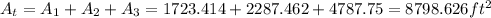
Explanation:
We assume that the plot attaced is the illustration for the problem.
For this case we need to begin finding the values for x and y using the cosine law given by:
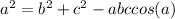
We can begin finding the value of x like this:

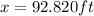
And similar in order to find the value of y we got this:
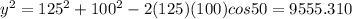

We can find the area for the 3 triangls on this way, beggining from the left triangle:
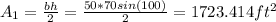
For the traingel in the most left part we have this:
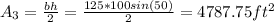
We obtain this value because if we find the angle a we got:
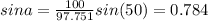
And then the angle a = 51.60 and for b = 180-51.60-50=78.402 degrees
Then we can create two equations in terms of h like this:
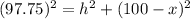
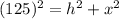
If we subtract both equation we got this:

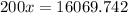
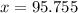
And then the area is just
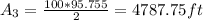
For the middle area we can begin finding the midsegment like this:
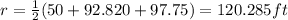
And now we can find the area 2 like this:

And then we just need to add the areas and we got: