Question

Use a table to aid in finding the product of (2x + 1)(x + 4).

Answer 1

`(2x+1) (x+4) = 2x^2 + 9x +8`

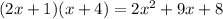
And then that's our final solution for this case.

Explanation:

One way to solve this problem is using the following property:

`(a+b) (c+d) = ac + ad + bc+bd`

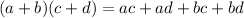
On this case we know that if we compare this formula with our expression (2x+1) (x+4) we have this:

a= 2x, b =1 , c= x , d = 4

We can find the individual products like this:

`ac= 2x* x = 2x^2`

`ad= 2x*4 = 8x`

`bc= 1*x = x`

`bd = 1*4 = 8`

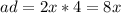
Then if we replace the values we got:

`(2x+1) (x+4) = 2x^2 + 8x +x+8`

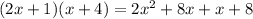
And we can add the two common factors 8x and x like this:

`(2x+1) (x+4) = 2x^2 + 9x +8`

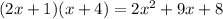
And then that's our final solution for this case.