Answer:
 is at
is at
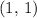 .
.
 is at
is at
 .
.
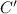 is at
is at
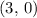 .
.
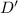 is at
is at
 .
.
Explanation:
To reflect a shape about the
 -axis, simply reflect each of its vertex across the
-axis, simply reflect each of its vertex across the
 -axis.
-axis.
The
 -coordinate of a point gives the vertical position of the point. On the other hand, the
-coordinate of a point gives the vertical position of the point. On the other hand, the
 -axis is horizontal. Reflecting the point would invert the
-axis is horizontal. Reflecting the point would invert the
 -coordinate of that point.
-coordinate of that point.
For example, reflecting
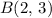 about the
about the
 -axis would give
-axis would give
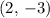 .
.
Similarly, to move the polygon up by
 units, simply move every one of its vertex up by
units, simply move every one of its vertex up by
 units. Keep in mind that the order of the translation does matter. In this question, reflect each point before moving them upward.
units. Keep in mind that the order of the translation does matter. In this question, reflect each point before moving them upward.
To move a point up by
 units, simply
units, simply
 to its
to its
 -coordinate. Aftering moving
-coordinate. Aftering moving
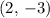 , the reflection of
, the reflection of
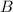 , up by two units, the new point would have coordinates
, up by two units, the new point would have coordinates
 .
.
 .
.