Question

Use appropriate identities to rewrite the wave equation shown below in the form ℎ(x) = a cos (x − c).

ℎ(x) = 6 sin(x) + 8 cos(x)

Answer 1

`h(x) = 10 cos(x-36.870)`

Explanation:

Note: For this problem we use the calculator on degrees

For this case we need to remember this identity :

`Cos (a-b) = cos a cos b + sin a sin b`

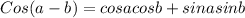
For this case if we apply for our desired formula we got this:

`a cos (x-c) = a [cos (c) cos (x) + sin (c) sin (x)]`

And we want this equal to
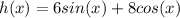`h(x) = 6 sin (x) + 8 cos (x)` so we can set up the following equality:

`6 sin (x) + 8 cos (x)= a cos (c) [cos (x)] + a sin (c) [sin(x)]` (1)

If we apply direct comparison between the factors on equation (1) we see this:

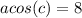`a cos(c) = 8` (2)

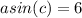`a sin (c) = 6` (3)

If we solve a from equation (2) we got:

`a = (8)/(cos (c))` (4)

If we replace equation (4) into equation (3) we got:

`(8)/(sin(c)) cos (c) = 8 tan (c) = 6`

`tan(c) = (6)/(8)=(3)/(4)`

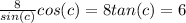
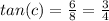
If we apply inverse tangent on both sides we got:

`c = tan^(-1) (3/4) = 36.870`

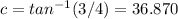
So then the value of c= 36.870 degrees. And since w ehave the value of c we can find the value for a and we got:

`[tex] a = (8)/(cos (36.870))=10`

And then our expression in the form
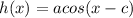`h(x) = a cos (x-c)` is:

`h(x) = 10 cos(x-36.870)`

And we can check that:

`h(x)= 10 cos (36.870) [cos (x)] + 10 sin (36.870) [sin(x)]= 8 cos (x) + 6 sin (x)`