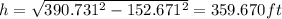Answer:
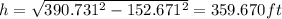
Explanation:
The situation is illustrated on the figure attached.
We can begin finding the values for h1 and h2 and in order to do this we can use the sine law.

From this we have that
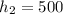
And for h1 we have this:
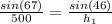
And we got
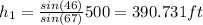
Now we cna use the Pythagorean identity, since we have two right triangles. If we apply this identity to the right triangle on the left we have this:
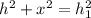 (1)
(1)
And for the right triangle we got:
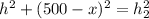 (2)
(2)
We can subctract equation (2) and (1) and we got:
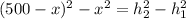
And if we apply some algebra we got this:
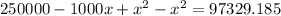
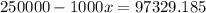
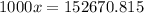
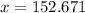
Now since we have the value of x we can find the value for h like this: