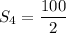Answer:
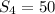
Explanation:
Sum Of Arithmetic Sequence
Given an arithmetic sequence
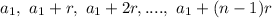
The sum of the n first terms is
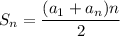
Or equivalently
![\displaystyle S_n=([2a_1+(n-1)r]n)/(2)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rj3nfo87iu7k8axg35u92b31hkbnws29go.png)
The given sequence is
5, 8, 11 ...
We can see the common difference between terms is r=3
We are asked to find the sum of the terms 2 to 5, it means that
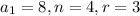
![\displaystyle S_4=([2(8)+(4-1)3]4)/(2)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/a43pflzgdf3mt2kpnvyey72j8mvbb0dkvi.png)