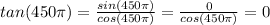Answer:
a) We can remove the complete rotations around the unitary circle like this, because we know that one complete revolution is equivalent to
 :
:
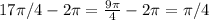
For this case we know that
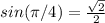
So then
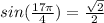
b) We can remove the complete rotations around the unitary circle like this, because we know that one complete revolution is equivalent to
 :
:
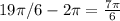
For this case we know that
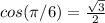
And we know that
 is on the III quadrant since is equivalent to 210 degrees. And on the III quadrant the cosine is negative. So then
is on the III quadrant since is equivalent to 210 degrees. And on the III quadrant the cosine is negative. So then

c) For this case that any factor of
 the sin function is equal to 0.
the sin function is equal to 0.
So from definition of tan we have this:
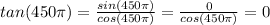
Explanation:
a. sin (17pi / 4 )
We can remove the complete rotations around the unitary circle like this, because we know that one complete revolution is equivalent to
 :
:
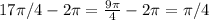
For this case we know that
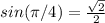
So then
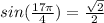
b. cos (19pi / 6 )
We can remove the complete rotations around the unitary circle like this, because we know that one complete revolution is equivalent to
 :
:
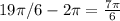
For this case we know that
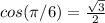
And we know that
 is on the III quadrant since is equivalent to 210 degrees. And on the III quadrant the cosine is negative. So then
is on the III quadrant since is equivalent to 210 degrees. And on the III quadrant the cosine is negative. So then

c. tan(450pi)
For this case that any factor of
 the sin function is equal to 0.
the sin function is equal to 0.
So from definition of tan we have this: