Question

Use the identity tan(theta) = sin(theta) / cos(theta) to show that tan(???? + ????) = tan(????)+tan(????) / 1−tan(????) tan(????)

.

Answer 1

See the proof below.

Explanation:

For this case we need to proof the following indentity:

`tan(x+y) = (tan (x) + tan(y))/(1- tan(x) tan(y))`

So we need to begin with the definition of tangent, we know that
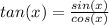`tan (x) =(sin(x))/(cos(x))` and we can do this:

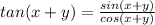`tan (x+y) = (sin (x+y))/(cos(x+y))` (1)

We also have the following identities:

`sin (a+b) = sin (a) cos(b) + sin (b) cos(a)`

`cos(a+b)= cos(a) cos(b) - sin(a) sin(b)`

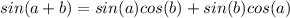
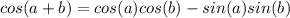
Now we can apply those identities into equation (1) like this:

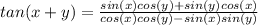`tan (x+y) =(sin (x) cos(y) + sin (y) cos(x))/(cos(x) cos(y) - sin(x) sin(y))` (2)

We can divide numerator and denominator from expression (2) by
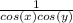`(1)/(cos(x) cos(y))` we got this:

`tan (x+y) = ((sin (x) cos(y))/(cos (x) cos(y)) + (sin(y) cos(x))/(cos(x) cos(y)))/((cos(x) cos(y))/(cos(x) cos(y)) -(sin(x)sin(y))/(cos(x) cos(y)))`

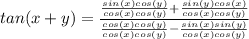
And simplifying we got:

`tan (x+y) = (tan(x) + tan(y))/(1-tan(x) tan(y))`

And that complete the proof.