Question

Using the general formula for perpendicularity of segments with one endpoint at the origin, determine if

the segments from the given points to the origin are perpendicular.
a. (4, 10), (5, −2)
b. (−7, 0), (0, −4)
c. Using the information from part (a), are the segments through the points (−3, −2), (1, 8), and
(2, −4) perpendicular? Explain.

Answer 1

a. perpendicular

b. perpendicular

c. perpendicular

Explanation:

The condition for two lines to be perpendicular is:

`m_(1)m_(2)=-1`

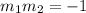
where
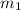`m_(1)` is the slope of one line and
`m_(2)` the slope of the other line.

How we calculate the slope? if we have two points
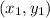`(x_(1),y_(1))` and
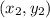`(x_(2),y_(2))` the slope of the line between them is:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

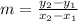
according to the problem the end point of all the lines for part a and par b is the origin, so
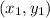`(x_(1),y_(1))` will be
`(0,0)`

• part a,

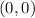
lets calculate the slope of the line that passes between (0, 0) and (4,10), in this case

`x_(1)=0\\y_(1)=0\\x_(2)=4\\y_(2)=10`

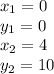
so the first slope is:

`m_(1)=(10-0)/(4-0)=(10)/(4)`

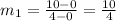
and for the line that passes between the ponits (0,0 ) and (5, -2)

`x_(1)=0\\y_(1)=0\\x_(2)=5\\y_(2)=-2`

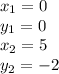
so the second slope is:

`m_(2)=(-2-0)/(5-0)=(-2)/(5)`

Now let's check if they are perpendicular:

`m_(1)m_(2)=-1`

`((10)/(4) )((-2)/(5) )=(-20)/(20) =-1`

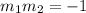
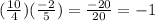
meets the condition, the lines in part a are perpendicular

• part b

we have the point: (-7,0) this is on the x-axis, the line with the origin is horizontal

and we have the point (0,-4) this is on the y-axis, the line with the origin is vertical.

Since one line is horizontal and the other vertical, the lines in part b are also perpendicular

• part c

the line between (-3,-2) and (1,8) has a slope:

`m_(1)=(8+2)/(1+3)=(10)/(4)`

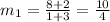
the line between (-3,-2) and the origin (2,-4) has a slope:

`m_(2)=(-4+2)/(2+3)=(-2)/(5)`

Now let's check if they are perpendicular:

`m_(1)m_(2)=-1`

`((10)/(4) )((-2)/(5) )=(-20)/(20)=-1`

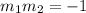
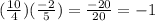
the lines are perpendicular.