Question

Verify the identity sin (x + ???? / 2) = cos(x) for all real numbers x by using a graph.

Answer 1

See proof and explanation below.

Explanation:

First we can proof this analitically first using the following property:

`sin(a+b) = sin(a) cos(b) + sin (b) cos(a)`

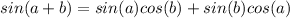
If we apply this into our formula we got:

`sin (x + (\pi)/(2)) = sin (x) cos((\pi)/(2)) + sin ((\pi)/(2)) cos (x)`

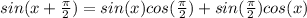
And if we simplify we got:

`sin (x + (\pi)/(2)) = sin ((\pi)/(2)) cos (x)= cos (x)`

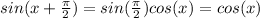
And that complete the proof.

If we analyze the graphs sin(x) and cos (x) we see that we have a gap between two graphs of
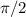`\pi/2` as we can see on the figure attached.

When we do the transformation
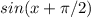`sin(x +\pi/2)` we are moving to the left
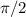`\pi/2` units and then would be exactly the cos function.