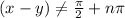Question

Verify the identity tan(???? − ????) = tan(????)−tan(????) / 1+tan (????) tan(????) for all (???? − ????) ≠ ???? / 2 + ????n.

Answer 1

See the proof below.

Explanation:

For this case we need to proof the following identity:

`tan(x-y) = (tan x - tan y)/(1 + tan x tan y)`

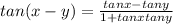
So we need to begin with the definition of tan, we know that
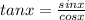`tan x = (sin x)/(cos x)` and we have this:

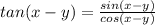`tan (x-y) = (sin(x-y))/(cos(x-y))` (1)

We also have the following identities:

`sin (a-b) = sin a cos b - sin b cos a`

`cos(a-b) = sin a sin b + cos a cos b`

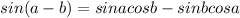
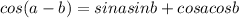
And if we apply those identities into equation (1) we got:

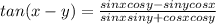`tan(x-y) = (sin x cos y - sin y cos x)/(sin x sin y + cos x cos y)` (2)

We can divide numerator and denominator from expression (2) by
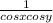`(1)/(cos x cos y)` like this:

`tan(x-y) = ((sin x cos y)/(cos x cos y) - (sin y cos x)/(cos x cos y))/((sin x sin y)/(cos x cos y) + (cos x cos y)/(cos x cos y))`

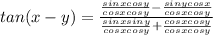
And if we simplity we got:

`tan(x-y) = (tan x - tan y)/(tan x tan y +1 )`

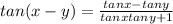
And with that we complete the proof. And that appies for all
`(x-y) \\eq (\pi)/(2) +n\pi`