Question

Without solving, determine the number of real solutions for each quadratic equation.

1. ????^2 − 4???? + 3 = 0
2. 2n^2 + 7 = −4n + 5
3. x − 3x^2 = 5 + 2x − x^2
4. 4???? + 7 = ????^2 − 5???? + 1

Answer 1

1. x^2 − 4x + 3 = 0

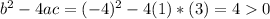`b^2 -4ac = (-4)^2 -4(1)*(3)= 4 >0` So we have two real solutions

2. 2n^2 + 7 = −4n + 5

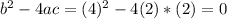`b^2 -4ac = (4)^2 -4(2)*(2)= 0` So we just one real solution

3. x − 3x^2 = 5 + 2x − x^2

`b^2 -4ac = (1)^2 -4(2)*(5)= -19 <0` No real solutions

4. 4x + 7 = x^2 − 5x + 1

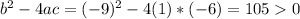`b^2 -4ac = (-9)^2 -4(1)*(-6)= 105 >0` So we have two real solutions

Explanation:

1. x^2 − 4x + 3 = 0

We need to compare this function with the general equation for a quadratic formula given by:

`f(x) = ax^2 + bx + c`

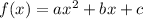
On this case we see that a=1, b = -4 and c =3

We can find the discriminat with the following formula:

`√(b^2 -4ac)`

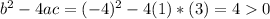`b^2 -4ac = (-4)^2 -4(1)*(3)= 4 >0` So we have two real solutions

2. 2n^2 + 7 = −4n + 5

We can rewrite the expression like this:

`2n^2 +4n +2`

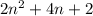
On this case we see that a=2, b = 4 and c =2

We can find the discriminat with the following formula:

`√(b^2 -4ac)`

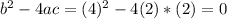`b^2 -4ac = (4)^2 -4(2)*(2)= 0` So we just one real solution

3. x − 3x^2 = 5 + 2x − x^2

We can rewrite the expression like this:

`2x^2 +x +5`

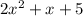
On this case we see that a=2, b = 1 and c =5

We can find the discriminat with the following formula:

`√(b^2 -4ac)`

`b^2 -4ac = (1)^2 -4(2)*(5)= -19 <0` No real solutions

4. 4x + 7 = x^2 − 5x + 1

We can rewrite the expression like this:

`x^2 -9x -6`

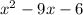
On this case we see that a=1, b = -9 and c =-6

We can find the discriminat with the following formula:

`√(b^2 -4ac)`

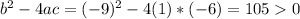`b^2 -4ac = (-9)^2 -4(1)*(-6)= 105 >0` So we have two real solutions