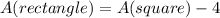Answer:

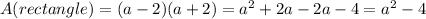
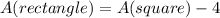
Explanation:
For this case we assume that the square have sides of length x.
So then the area for this square is given by

We have a rectangle and on this case we have this information :" the rectangle has side lengths 2 less and 2 more than a square"
So then the sides of the rectangle needs to have lengths a-2 and a+2, and if we find the area for the rectangle we got:
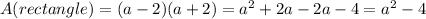
And as we can see th area for the rectangl is 4 units less than the area for the rectangle: