Answer:
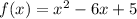
Explanation:
The general form of quadratic function is
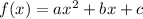 .... (1)
.... (1)
It is given that the function defined by the points (0, 5), (5, 0), and (3, −4). It means the function must be satisfied by these points.
For (0,5),
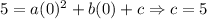
The value of c is 5.
For (5,0),
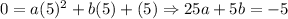 .... (2)
.... (2)
For (3,-4),
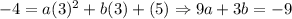 .... (3)
.... (3)
Multiply equation (2) by 3 and equation (3) by 5.
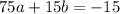 .... (4)
.... (4)
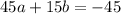 .... (5)
.... (5)
Subtract equation (5) from equation (4).
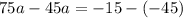
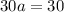
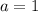
Substitute a=1 in equation (3).
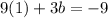
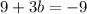
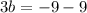
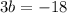
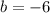
Substitute a=1,b=-6 and c=5 in equation (1).
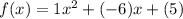
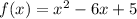
Therefore, the required function is
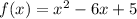 .
.