Answer:
Roger should place the base of ladder approximately 5.7 m away from base of building to reach the window.
Explanation:
Given,
Length of ladder = 9 m
We have to find that how far Roger should place the base of ladder to reach the window.
Solution,
We have drawn the diagram for your reference.
Here the building, the ladder on leaning with land makes a right angle triangle.
Where the length of ladder is 'hypotenuse'.
Height of window from the ground is 'one side of the triangle'.
And distance from base of building to the ladder is 'another side of the triangle'.
So, according to Pythagoras theorem;
"In a right angled triangle the square of the hypotenuse is equal to the sum of the squares of other two sides".
On framing in equation form, we get;
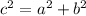
Where 'a' = 1st side of right triangle =7 m
'b' = 2nd side of right triangle
'c' = hypotenuse = 9 m
Now we put the given values and get;
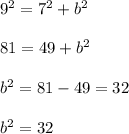
Now taking square root on both side, we get;

Hence Roger should place the base of ladder approximately 5.7 m away from base of building to reach the window.