Question

Without using a graphing calculator, sketch the graphs of the functions below based on transformations of the

graph of the parent function ????????(xx) = xx2. Use your own graph paper, and label your graphs.
a. ????(x) = (x + 2)^2 − 4
b. ℎ(x) = −(x − 4)^2 + 2
c. ????(x) = 2x^2 − 12x + 19
d. p(x) = −2x^2 − 4x − 5
e. ????(x) = 3x^2 + 6x

Answer 1

See explanation and figures below.

Explanation:

a. h(x) = (x + 2)^2 − 4

For this case the original function is
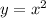`y = x^2` with a vertex (0,0) for the new function we have the following general expression
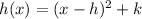`h(x)= (x-h)^2 + k` on this case we see that h = -2 and k =-4 so then the vertex for the new function would be (-2,4), and the x intercepts are (-4,0) and (0,0) as we can see on the figure attached 1.

b. ℎ(x) = −(x − 4)^2 + 2

For this case the original function is
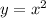`y = x^2` with a vertex (0,0) for the new function we have the following general expression
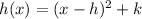`h(x)= (x-h)^2 + k` on this case we see that h = 4 and k =2 so then the vertex for the new function would be (4,2), and the x intercepts are (2.586,0) and (5.414,0) as we can see on the figure attached 2.

On this case since we have a negative on the quadratic term we see that the parabola would open downwards.

c. h(x) = 2x^2 − 12x + 19

For this case after the first transformation
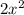`2x^2` we have a compression on the x axis, the -12x would cause that the function move to the right and upward and an expansion on the x axis. And finally the +19 cause that the function moves upward 19 units. The new vertex would be (3,1) and we just have one y intercept (0,19) and none x intercepts. We see the plot on figure 3.

d. p(x) = −2x^2 − 4x − 5

For this case after the first transformation
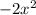`-2x^2` we have a compression on the x axis and the parabola would open downwards, the -4x would cause that the function move to the left and down and an expansion on the x axis. And finally the -5 cause that the function moves downward 5 units. The new vertex would be (-1,3) and we just have one y intercept (0,-5) and none x intercepts. We see the plot on figure 4.

e. h(x) = 3x^2 + 6x

For this case after the first transformation
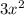`3x^2` we have a compression on the x axis, the +6x would cause that the function move to the left and down and an expansion on the x axis. The new vertex would be (-1,-3) and the x intercepts would be:

`3x(x+2) = 0`

`x=0 , x=-2`

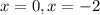
And we can see the plot on figure 5 attached.