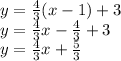Answer:
a.
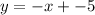
b.
Explanation:
to solve part a we have the slope of the line and a point, so we use the point-slope equation

where
 is the slope:
is the slope:
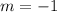 , and
, and
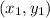 is the point, so in this case the point is
is the point, so in this case the point is
 thus
thus
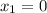 and
and
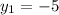 .Thus the equation is:
.Thus the equation is:

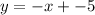
And for part b we have two points. With the two points we can find the slope and then use the point-slope equation again.
To find the slope we use:
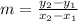
for the points
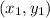 and
and
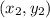 . Since we have the poits:
. Since we have the poits:
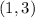 and
and
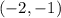
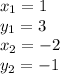
Thus, the slope:
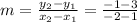
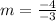

and now using the point-slope equation: