Answer:
The graph of parent function reflected across x-axis, vertically stretched by factor 2 and shift 5 units left 3 units down.
Step-by-step explanation:
The parent function is
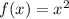
The given function is
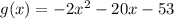
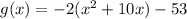
If an expression is
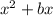 , then we have to add
, then we have to add
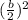 in it to make it perfect square.
in it to make it perfect square.
In the parenthesis the value of b is 10.
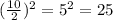
Add and subtract 25 in the parenthesis.
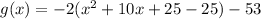
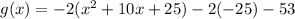
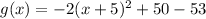
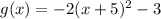
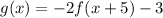 .... (1)
.... (1)
The translation is defined as
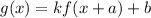 .... (2)
.... (2)
Where, k is stretch factor, a is horizontal shift and b is vertical shift.
If 0<|k|<1, then the graph compressed vertically by factor k and if |k|>1, then the graph stretch vertically by factor k.
Negative k represents the reflection across x-axis.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.
From (1) and (2) it is clear that k=-2, a=5 and b=-3.
It means graph of parent function reflected across x-axis, vertically stretched by factor 2 and shift 5 units left, 3 units down.