Question

Write the function ????(x) = −2x^2 − 20x − 53 in completed-square form. Describe the transformations of the graph

of the parent function ????(x) = x^2 that result in the graph of ????.

Answer 1

The graph of parent function reflected across x-axis, vertically stretched by factor 2 and shift 5 units left 3 units down.

Step-by-step explanation:

The parent function is

`f(x)=x^2`

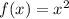
The given function is

`g(x)=-2x^2-20x-53`

`g(x)=-2(x^2+10x)-53`

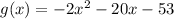
If an expression is
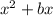`x^2+bx`, then we have to add
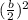`((b)/(2))^2` in it to make it perfect square.

In the parenthesis the value of b is 10.

`((10)/(2))^2=5^2=25`

Add and subtract 25 in the parenthesis.

`g(x)=-2(x^2+10x+25-25)-53`

`g(x)=-2(x^2+10x+25)-2(-25)-53`

`g(x)=-2(x+5)^2+50-53`

`g(x)=-2(x+5)^2-3`

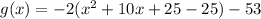
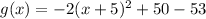
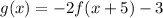`g(x)=-2f(x+5)-3` .... (1)

The translation is defined as

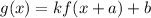`g(x)=kf(x+a)+b` .... (2)

Where, k is stretch factor, a is horizontal shift and b is vertical shift.

If 0<|k|<1, then the graph compressed vertically by factor k and if |k|>1, then the graph stretch vertically by factor k.

Negative k represents the reflection across x-axis.

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

From (1) and (2) it is clear that k=-2, a=5 and b=-3.

It means graph of parent function reflected across x-axis, vertically stretched by factor 2 and shift 5 units left, 3 units down.