Question

A person is standing on a cliff that is 200ft above a body of water. The person looks down at an angle of depression of 42o at a sailboat. Then the person looks at a yacht that is further out at an angle of depression of 15o. What is the distance (in feet) between the sailboat and the yacht?

Answer 1

524.5 feet

Explanation:

Given: Height of cliff= 200 ft

Angle of depression at sail boat is 42°

Angle of depression at yacht is 15°

Lets assume distance sailboat from the bottom of cliff is "
`d_1`"

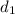And assume distance yacht from the bottom of cliff is "
`d_2`"

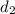Now using tangent rule to solve it.

we know,
`tan\theta = (opposite)/(adjacent)`

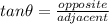
Distance sailboat from the bottom of cliff;
`tan 42= (200)/(d_1)`

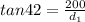
Using trignometry table to know the value of tan 42°

⇒
`0.90= (200)/(d_1)`

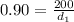
cross multiplying both side.

⇒
`d_1= (200)/(0.90) = 222.22 \approx 222`

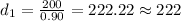
∴ Distance sailboat from the bottom of cliff (
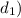`d_1)`= 222 feet

Distance yatch from the bottom of cliff;
`tan 15= (200)/(d_2)`

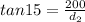
Using trignometry table to know the value of tan 15°

⇒
`0.2679= (200)/(d_2)`

cross multiplying both side.

⇒
`d_2= (200)/(0.2679) = 746.54 \approx 746.5`

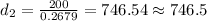
∴Distance yacht from the bottom of cliff
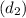`(d_2)`= 746.5 feet.

Next, finding the distance between sailboat and yacht.

Distance between sailboat and yacht =
`d_2-d_1`

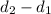
⇒ Distance between sailboat and yacht=
`746.5-222= 524.5\ ft`

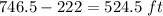
∴ Distance between sailboat and yacht is 524.5 feet.