Question

A 15-ft ladder rests against a vertical wall. If the top of the ladder slides down the wall at a rate of 0.33 ft/sec, how fast, in ft/sec, is the bottom of the ladder sliding away from the wall, at the instant when the bottom of the ladder is 9 ft from the wall? Answer with 2 decimal places. Type your answer in the space below. If your answer is a number less than 1, place a leading "0" before the decimal point (ex: 0.35)

Answer 1

0.44 ft/sec.

Explanation:

Let A is the bottom of the ladder and AB is the distance from the bottom of the wall i.e. B is the bottom of the wall. If C is the top of the ladder and BC is the height of the wall.

Now, Δ ABC is a right triangle and AC is the length of the ladder i.e. hypotenuse.

Now, AC² = AB² + BC² {From Pythagoras Theorem}

Now, differentiating both sides with respect to time t, we get

`0 = 2 * (AB) * (d(AB))/(dt) +  2 * (BC) * (d(BC))/(dt)`

⇒
`(d(AB))/(dt) = - (BC)/(AB) *  (d(BC))/(dt)`

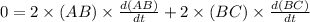
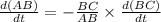
Now, given that
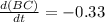`(d(BC))/(dt) = - 0.33` feet/sec.

Hence,
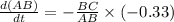`(d(AB))/(dt) = - (BC)/(AB) *  (- 0.33)` ......... (1)

Now, given that AB = 9 ft. and AC = 15 ft.

So, 15² = 9² + BC²

⇒ BC² = 144

⇒ BC = 12 feet.

Now, from equation (1), we get

`(d(AB))/(dt) = - (12)/(9) *  (- 0.33) = 0.44`

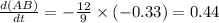
Therefore, the bottom of the ladder is sliding away from the wall at the rate of 0.44 ft/sec. (Answer)