Question

The product of two consecutive odd integers is 99. If

x
is the smallest of the integers, write an equation in terms of
x
that describes the situation, and then find all such pairs of integers.

Answer 1

The equation in terms of x is x(x + 2) = 99 or
`x^2 + 2x - 99 = 0`

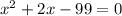
The pairs of integers are -11 and -9 or 9 and 11

Solution:

Let the two consecutive odd integers be x and x + 2

Let "x" be the smallest integer

Given that product of two consecutive odd integers is 99

To find: an equation in terms of x

Product of x and x + 2 = 99

`x(x + 2) = 99\\\\x^2 + 2x = 99\\\\x^2 + 2x - 99 = 0`

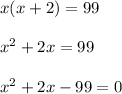
Thus the equation in terms of x is found

Let us solve the above equation to find all pairs of integers

Solve the quadratic equation by grouping method

Middle term 2x can be written as 11x - 9x

`\rightarrow x^2 + 2x - 99 = 0\\\\\rightarrow x^2 + 11x - 9x -99 = 0`

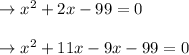
Now group the terms,

`\rightarrow (x^2 + 11x) - (9x + 99) = 0`

Take "x" as common term from first group and 9 as common term from second group

`\rightarrow x(x + 11)-9(x+ 11) = 0`

Now take x + 11 as common term,

`\rightarrow (x + 11)(x - 9) = 0`

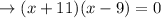
Equating to zero we get,

x + 11 = 0 or x - 9 = 0

x = -11 or x = 9

When x = -11 :

x + 2 = -11 + 2 = -9

Thus first set of two consecutive odd integers are -11 and -9

When x = 9 :

x + 2 = 9 + 2 = 11

Thus second set of two consecutive odd integers are 9 and 11