Question

The rectangle shown has a perimeter of 58 cm and the given area. Its length is 8 more than twice its width. Write and solve a system of equations to find the dimensions of the rectangle. The area is 154cm squared

Answer 1

`L = 8 + 2w`

`58=2(L+w)`

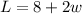
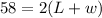
The length of the rectangle is 22 cm and width is 7 cm.

Explanation:

Let the width of the rectangle be 'w'.

Given:

Perimeter (P) = 58 cm

Area of the rectangle (A) = 154 cm²

As per question:

Length = 8 more than twice its width

`L = 8 + 2w----- 1`

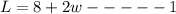
Now, perimeter is given as:

`P=2(L+w)\\\\58=2(L+w)\\\\29=L+w----- 2`

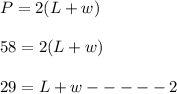
Now, we have to solve the given system of equations.

For that, we plug in 'L' from equation 1 to equation 2. This gives,

`29=8+2w+w\\\\29=8+3w\\\\29-8=3w\\\\21=3w\\\\3w=21\\\\w=(21)/(3)=7\ cm`

`L=8+2w\\\\L=8+2(7)=8+14=22\ cm`

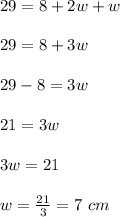
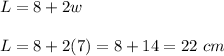
Therefore, the length of the rectangle is 22 cm and width is 7 cm.

Area = Length × Width = 22 × 7 = 154 cm².