Answer:
Graph 4
Explanation:
When being asked problems like this one, even before working out any specifics, looking at the direction the line is moving in, you can at least eliminate some answers. When a graph has a negative slope, it will be decreasing as it moves to the right on the x-axis (its direction will look somewhat like a \, but not always this steep). Only two answers to this question have these properties, Graph 3 and Graph 4. Because of this trick, we're able to eliminate Graph 1 and Graph 2 as possible answers to this question, but how do we decide between Graph 3 and Graph 4? This is where knowledge on Linear Equations come into play.
 is the parent function for linear equations, and its properties are as follows:
is the parent function for linear equations, and its properties are as follows:
 is the equation's slope; determining the magnitude and direction of a linear line. Slope represents a ratio of how many units a function moves up or down to how much it moves left or right. For example, the equation
is the equation's slope; determining the magnitude and direction of a linear line. Slope represents a ratio of how many units a function moves up or down to how much it moves left or right. For example, the equation
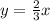 has a slope of
has a slope of
 . If the numerator of the function,
. If the numerator of the function,
 , represents how far the function moves upwards, and the denominator of the function,
, represents how far the function moves upwards, and the denominator of the function,
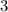 , represents its movement to the right, then for every 2 units the function goes upwards, that's 3 units to the right. If there were negative values in the slope (ex:
, represents its movement to the right, then for every 2 units the function goes upwards, that's 3 units to the right. If there were negative values in the slope (ex:
 ), then one of the directions would be down, or left.
), then one of the directions would be down, or left.
 represents the linear function's y-intercept; the y value it hits on the y-axis. For example, the equation
represents the linear function's y-intercept; the y value it hits on the y-axis. For example, the equation
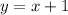 will hit the y axis at the point (0,1). This will help us finish solving the equation.
will hit the y axis at the point (0,1). This will help us finish solving the equation.
Looking at the two remaining graphs and using our knowledge on
 , we can see that Graph 3 hits the y-axis above
, we can see that Graph 3 hits the y-axis above
 and Graph 4 hits the y-axis below
and Graph 4 hits the y-axis below
 . If this problem is asking for the graph to have the same y-intercept as
. If this problem is asking for the graph to have the same y-intercept as
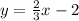 , then with
, then with
 being
being
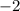 , we can figure that the function we want to make will have to hit the y-axis at
, we can figure that the function we want to make will have to hit the y-axis at
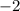 , below
, below
 . Only Graph 4 has these properties, so it is the answer.
. Only Graph 4 has these properties, so it is the answer.