Question

Is 1/3, 2/3, 4/3, 8/3, 16/3 arithmetic sequence

Answer 1

The given sequence is not arithmetic sequence

Solution:

Given sequence is:

`(1)/(3) , (2)/(3) , (4)/(3) , (8)/(3) , (16)/(3)`

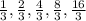
We have to find if the above sequence is arithmetic sequence or not

An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant

Here in the given sequence

`\text{ first term } = a_1 = (1)/(3)\\\\\text{ second term } = a_2 = (2)/(3)\\\\\text{ third term } = a_3 = (4)/(3)\\\\\text{ fourth term } = a_4 = (8)/(3)\\\\\text{ fifth term } = a_5 = (16)/(3)`

Let us find the difference between terms

`a_2 - a_1 = (2)/(3) - (1)/(3) = (1)/(3)`

`a_3 - a_2 = (4)/(3) - (2)/(3) = (2)/(3)`

`a_4 - a_3 = (8)/(3) - (4)/(3) = (4)/(3)`

`a_5 - a_4 = (16)/(3) - (8)/(3) = (8)/(3)`

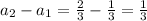
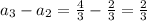
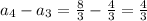
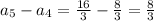
Thus the difference between terms is not constant

So the given sequence is not arithmetic sequence