Question

John, Joe, and James go fishing. At the end of the day, John comes to collect his third of the fish. However, there is one too many fish to make equal thirds, so John throws it out, takes his third and leaves. Joe comes to get his fish without realizing John has already taken his third. He notices that there is one too many fish to make equal thirds, so he throws one out, takes his fish and leaves. James notices that there is one too many fish to make equal thirds, so he throws one out, takes his fish and leaves. Assuming no fish are divided into pieces, what is the minimum possible number of fish before John threw out the first fish?

Answer 1

The minimum possible initial amount of fish:
`52`

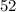
Explanation:

Let's start by saying that

`x` = is the initial number of fishes

John:

When John arrives:

• he throws away one fish from the bunch

`x-1`

• divides the remaining fish into three.

`(x-1)/(3) + (x-1)/(3) + (x-1)/(3)`

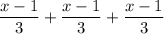
• takes a third for himself.

`(x-1)/(3) + (x-1)/(3)`

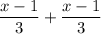
the remaining fish are expressed by the above expression. Let's call it John

`\text{John}=(x-1)/(3) + (x-1)/(3)`

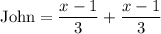
and simplify it!

`\text{John}=(2x)/(3) - (2)/(3)`

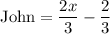
When Joe arrives:

• he throws away one fish from the remaining bunch

`\text{John} -1`

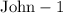
• divides the remaining fish into three

`\frac{\text{John} -1}{3} + \frac{\text{John} -1}{3} + \frac{\text{John} -1}{3}`

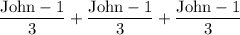
• takes a third for himself.

`\frac{\text{John} -1}{3}+ \frac{\text{John} -1}{3}`

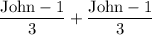
the remaining fish are expressed by the above expression. Let's call it Joe

`\text{Joe}=\frac{\text{John} -1}{3}+ \frac{\text{John} -1}{3}`

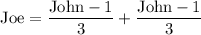
and simiplify it

`\text{Joe}=(2)/(3)(\text{John}-1)`

since we've already expressed John in terms of x, we express the above expression in terms of x as well.

`\text{Joe}=(2)/(3)\left((2x)/(3) - (2)/(3)-1\right)`

`\text{Joe}=(4x)/(9) - (10)/(9)`

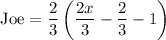
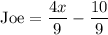
When James arrives:

We're gonna do this one quickly, since its the same process all over again

`\text{James}=\frac{\text{Joe} -1}{3}+ \frac{\text{Joe} -1}{3}`

`\text{James}=(2)/(3)\left((4x)/(9) - (10)/(9)-1\right)`

`\text{James}=(8x)/(27) - (38)/(27)`

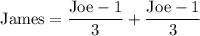
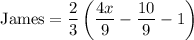
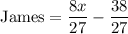
This is the last remaining pile of fish.

We know that no fish was divided, so the remaining number cannot be a decimal number. We also know that this last pile was a multiple of 3 before a third was taken away by James.

Whatever the last remaining pile was (let's say
`n`), a third is taken away by James. the remaining bunch would be
`(n)/(3)+(n)/(3)`

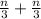
hence we've expressed the last pile in terms of n as well. Since the above 'James' equation and this 'n' equation represent the same thing, we can equate them:

`(n)/(3)+(n)/(3)=(8x)/(27) - (38)/(27)`

`(2n)/(3)=(8x)/(27) - (38)/(27)`

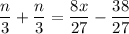
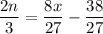
L.H.S must be a Whole Number value and this can be found through trial and error. (Just check at which value of n does 2n/3 give a non-decimal value) (We've also established from before that n is a multiple a of 3, so only use values that are in the table of 3, e.g 3,6,9,12,..

at n = 21, we'll see that 2n/3 is a whole number = 14. (and since this is the value of n to give a whole number answer of 2n/3 we can safely say this is the least possible amount remaining in the pile)

`14=(8x)/(27) - (38)/(27)`

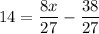
by solving this equation we'll have the value of x, which as we established at the start is the number of initial amount of fish!

`14=(8x)/(27) - (38)/(27)`

`x=52`

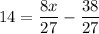
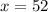
This is minimum possible amount of fish before John threw out the first fish