Answer:
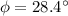
Step-by-step explanation:
We are given that
Capacitive reactance=
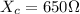
Resistance of circuit= R=
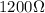
We have to find the phase angle between circuit voltage and current.
We know that
Phase angle,
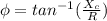
By using this formula we will find the phase angle between voltage and current of circuit.
Substitute the values then we get
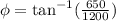
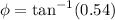
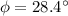
Hence, the phase angle between circuit voltage and current=28.4 degrees