Answer:
Each side of the fountain is 5 units
Explanation:
Given:
All the sides of the vertices are equal.
Vertices of the fountain
(7.5,5),
(11.5,2),
(7.5,−1),
(2.5,−1),
(−1.5,2),
(2.5,5)
To Find:
Length of the each side of the fountain = ?
Solution:
Let us find the Length of the hexagon using the distance formula
Distance formula =
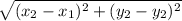
Now lets find the length of AB
Length of AB =
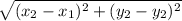
where
 = 7.5
= 7.5
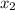 = 11.5
= 11.5
 = 5
= 5
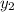 = 2
= 2
Substituting the values we get,
Length of AB =
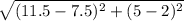
Length of AB =
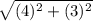
Length of AB =
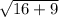
Length of AB =
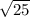
Length of AB = 5
Since all the sides of the hexagon are said to be equal, the length of the sides of the hexagon is 5 units