Question

1. Kyle and John are twins who decided to plan an imaginary trip that started with cliff jumping. There were two different spots to attempt a jump. Kyle took the spot 20 ft above the water. John jumped from the lower elevation, at 15 ft above the water.

(a) Kyle jumped from his starting point and went 15 ft below the surface of the water. Represent the starting point and the ending point as integers. What is the total distance he traveled? Explain how you got your answer.


(b) John jumped and went 10 ft below the surface of the water. Represent the starting point and the ending point as integers. What is the total distance he traveled? Explain how you got your answer.


(c) How much farther did Kyle travel than John? Use a number line to show how you got your answer.

Answer 1

I did a, b, and c but not d!

Explanation:

A. Kyle jumped off the cliff at 20 ft above sea level and landed -15 ft which is below sea level. Kyle traveled a total of 35 ft.

B. John jumped off the cliff at 15 ft above sea level and landed at 10 ft below sea level. John traveled 25 ft from the top of the cliff to 10 ft below sea level.

C. Kyle traveled 10 more ft than John because… 35 ft - 25 ft = 10.

I don't know what D is yet also hope this helped and please don't copy and paste this to your assignment!

Answer 2

a) Δx = -35ft

b) Δx = -25ft

c) Kyle traveled 10ft more than John

Explanation:

We define a coordinate reference system() in which y = 0 corresponds to the water surface.

a) The initial position of Kyle in our coordinate reference system is:

`x_(o) = 20 ft`

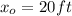
and his final position is:

`x_(f) = -15 ft`

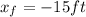
Therefore, he traveled

Δx =
`x_(f) - x_(o) = -15 - 20 = -35 ft`

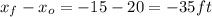
b) The initial position of John in our coordinate reference system is:

`x_(o) = 15 ft`

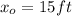
and his final position is:

`x_(f) = -10 ft`

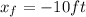
Therefore, he traveled

Δx =
`x_(f) - x_(o) = -10 - 15 = -25 ft`

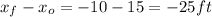
c) Then, Kyle traveled 10ft more than John