Answer with Step-by-step explanation:
1.In triangle ABC
AB=BC
Let AB=BC=x and AC=y
Perimeter of triangle ABC=25
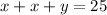
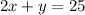 ...(1)
...(1)
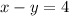 ...(2)
...(2)
Adding equation (1) and (2)
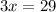
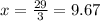
Substitute x=9.67 in equation (2)
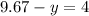

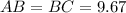
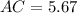
2.
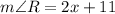
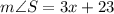

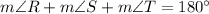
By using triangle angle sum property
Substitute the values then we get
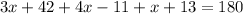
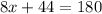

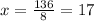
Substitute the value
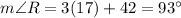
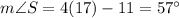
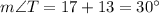
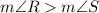
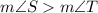
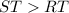 (Side ST is opposite to angle R, Side RT is opposite to angle S
(Side ST is opposite to angle R, Side RT is opposite to angle S
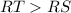 (side RS is opposite to angle T)
(side RS is opposite to angle T)
When a>b
Then , opposite side of a> opposite side of b
RS<RT<ST
3.
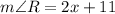
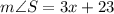
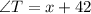
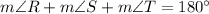
By using triangle angle sum property
Substitute the values then we get
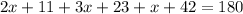
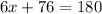
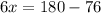
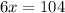
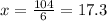
Substitute the value
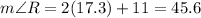
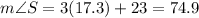
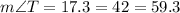
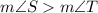
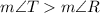
RT>RS
RS>ST
ST<RS<RT