Question

A Square Pyramid has a Total Surface Area of 264

square inches and the side length of its base is 12
inches. Determine the side length of its square base​

Answer 1

The slant height is 5 inches .

Explanation:

Given as :

The total surface area of square base pyramid =
`T_p` = 264 inches²

The side length of the square base pyramid = b = 12 inches

Let The slant height = h inches

Now, According to question

∵Total surface area of square base pyramid = area of the square base + area of each faces of triangle

So, Area of square base = side × side

i.e Area of square base = b × b

or, Area of square base = 12 inches × 12 inches

∴ Area of square base = 144 inches²

Again

Area of each faces of triangle

Since it has 4 triangle So, Area of 4 faces triangle = 4 ×
`(1)/(2)` × base × slant height

So, Area of 4 faces triangle = 2 × b × h

Or, Area of 4 faces triangle = 2 × 12 inches × h

or, Area of 4 faces triangle = 24 inches × h

So,Total surface area of square base pyramid = 144 inches² + 24 inches × h

or,
`T_p` = 144 inches² + 24 inches × h

Or, 264 inches² = 144 inches² + 24 inches × h

Or, 264 inches² - 144 inches² = 24 inches × h

Or, 120 inches² = 24 inches × h

∴ h =
`(120 )/(24)`

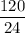
i.e h =5 inches

So, The slant height = h = 5 inches

Hence,The slant height is 5 inches . Answer