Question

A line passes through (3,-6) and (-7,-4) is parallel to a line represented by which of the following equations?

A. X+5y=6
B. X+1/2y=7
C. Y-2x=-9
D. 2y-x=-8

Answer 1

Option A is correct.

`X+5Y=6`

Explanation:

Given:

Two points are given (3,-6) and (-7,-4).

We need to find the line that is parallel to the line which is passes through the points (3,-6) and (-7,-4).

The slope of the line is.

`m = (y_(2)-y_(1) )/(x_(2)-x_(1) )`

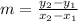
Now, we substitute all given value in above equation.

`m = (-4-(-6))/(-7-3)}`

`m = (-4+6))/(-10)}`

`m = (2))/(-10)}`

`m = -(1)/(5)`

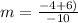
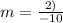
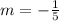
We know that the parallel lines has same slope, so we check the option one by one.

Option A,

`X+5Y=6`

Now, we write the above equation in standard form
`y=mx +c`.

`5Y=-X+6`

`Y = -(1)/(5)X+(6)/(5)`

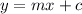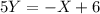
Where
`m = -(1)/(5)`

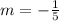
The slope of the above line is
`-(1)/(5)`, so the line
`X+5Y=6` is parallel to the line which is passes through the points (3,-6) and (-7,-4), so there is no need to check the other choices.

Therefore, Option A is correct.