Question

The base of a solid in the first quadrant of the xy plane is a right triangle bounded by the coordinate axes and the line x + y = 4. Cross sections of the solid perpendicular to the base are squares. What is the volume, in cubic units, of the solid?

A. 8
B. 32 divided by 3
C. 64 divided by 3
D. 64 divided by 3

Answer 1

64 divided by 3

Explanation:

Data provided in the question:

Equation of line : x + y = 4

Cross-section of the base is square

Now,

From x + y = 4

⇒ y = 4 - x

Therefore,

area of the base = ( 4 - x )² = x² + 16 - 8x

Thus,

volume , V = ₀∫⁴ [x² + 16 - 8x]dx

or

⇒ V =
`[(x^3)/(3)+16x -(8x^2)/(2)]_0^4`

or

⇒ V =
`[(4^3)/(3)+16(4) -(8(4)^2)/(2)]-[(0^3)/(3)+16(0) -(8(0)^2)/(2)]`

or

⇒ V =
`[(64)/(3)+64 -64]-0`

or

⇒ V =
`(64)/(3)`

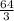
Hence,

Answer is 64 divided by 3