Answer:
The standard form of the parabola is
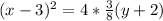
Explanation:
The standard form of a parabola is
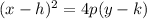 .
.
In order to convert
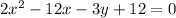 into the standard form, we first separate the variables:
into the standard form, we first separate the variables:
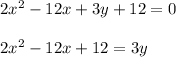
we now divided both sides by 2 to remove the coefficient from
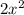 and get:
and get:
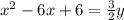 .
.
We complete the square on the left side by adding 3 to both sides:
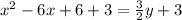
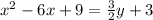
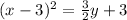
now we bring the right side into the form
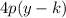 by first multiplying the equation by
by first multiplying the equation by
 :
:
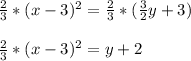
and then we multiplying both sides by
 to get
to get
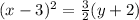 .
.
Here we see that
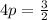
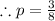
Thus, finally we have the equation of the parabola in the standard form:
