Answer:
Equation of the parabola with focus of (-3,3) and directrix y

Explanation:
As directix is not give so writing it in form of a.
Standard equation for parabola with directix is y = k - a and focus (h,k+a)
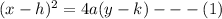
Given that focus is (-3, 3)
(-3, 3) = (h, k +a)
by comparison
h= -3
k+a = 3
a = 3 - a
Substituting this value in (1)
