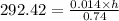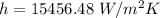Question

A fluid is flowing through a circulat tube at 0.4 kg/s. Tube inner surface is smooth with a diameter 0.014 m. Fluid density is 990 kg/m^3, specific heat is 3,845 J/(kg-K), viscosity is 0.00079 Ns/m^2, thermal conductivity is 0.74, and Prandtl number is 8.6. A uniform heat flux of 71,297 W/m^2 is supplied to the flow from the surface. If the flow is fully developed, what is the convection coefficient in W/(m^2-K)

Answer 1

The convection coefficient is
`15456.48\ W/m^(2)K`

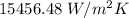
Solution:

Mass flow rate,
`\dot{m} = 0.4\ kg`

Inner diameter of the tube, d = 0.014 m

Fluid density,
`\rho_(f) = 990\ kg/m^(3)`

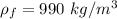
Specific Heat, C = 3845 J/K

Thermal Conductivity, K = 0.74

Prandtl Number,
`P_(r) = 8.6`

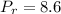
Heat flux,
`\dot{q} = 71,297\ W/m^(2)`

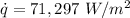
Viscosity,
`\mu = 0.00079\ Ns/m^(2)`

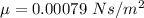
Now,

To calculate the convection heat coefficient, h:

Determine the cross sectional area of the circular tube:

`A_(c) = (\pi)/(4)d^(2) = (\pi)/(4)* (0.014)^(2) = 1.54\time 10^(- 4)\ m^(2)`

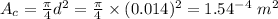
Determine the velocity of the fluid inside the tube by mass flow rate:

`\dot{m} = \rho_(f)A_(c)v`

`0.4 = 990* 1.54\time 10^(- 4)v`

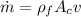
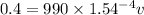
v = 2.624 m/s

Determine the Reynold's Number,
`R_(e)`:

`R_(e) = (\rho_(f)dv)/(\mu)`

`R_(e) = (990* 0.014* 2.624)/(0.00079) = 46036.253`

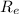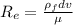
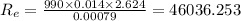
Thus it is clear that
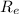`R_(e)` > 10,000 hence flow is turbulent.

Now,

Determine the Nusselt Number:

`N_(u) = 0.023R_(e)^(0.8)P_(r)^(0.4)`

`N_(u) = 0.023* 46036.253^(0.8)* 8.6^(0.4) = 292.42`

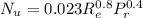
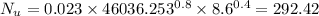
Also,

`N_(u) = (dh)/(K)`

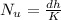
where

h = convection coefficient

Now,

`292.42 = (0.014* h)/(0.74)`

`h = 15456.48\ W/m^(2)K`