Question

(b) Gun sights are adjusted to aim high to compensate for the effect of gravity, effectively making the gun accurate only for a specific range. (a) A gun is sighted, meaning that it is set to shoot at a small angle, in this case 0.539° above the horizontal, to hit targets that are at the same height as the gun and 120.0 m away. How low will the bullet hit (in m below the target) if aimed directly at a target 165.0 m away? The muzzle velocity of the bullet is 250 m/s. Answer to 3 significant figures.

Answer 1

Case 1: The bullet will hit 2.134 meters below the target

Case 2: The bullet will hit 0.582 meters below the target

Step-by-step explanation:

Diagonal Launch

The problem describes a situation where a bullet is launched at a certain angle respect to the horizontal to hit in the target, given the launching conditions and the distance to the target. The formulas to compute the magnitudes involved in the projectile motion are

`X=V_o\ cos\theta \ t`

`\displaystyle Y=V_o\ sin\theta \ t-(gt^2)/(2)`

`\displaystyle X_m=(V_o^2\ sin2\theta)/(g)`

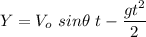
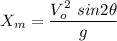
`X_m` is the maximum horizontal distance the object can reach when it returns to the ground (or launching height).

The first set of data is useless since we have enough information in the second part to compute the required distance. We'll only use the first part to check the validity of the data. Having:

`v_o=250\ m/s,\ \theta=0.539^o`,

let's check if X is computed correctly .

`\displaystyle X_m=(250^2\ sin2(0.539^o))/(9.8)\approx 120\ m`

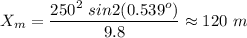
The set of data is correct. We can now proceed to the required distance. We know the bullet is shot directly to the target, so the angle is 0, keeping the same speed. The new maximum distance is 165 m, so we can compute the time needed to complete the flight

`\displaystyle Y=V_o\ sin\theta \ t-(gt^2)/(2)`

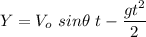
since
`\theta=0`

`\displaystyle Y=-(gt^2)/(2)`

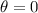
Let's find the time from the formula

`X=V_o\ cos\theta \ t`

`\displaystyle t=(X_m)/(V_ocos\theta)`

`\displaystyle t=(165)/(250)`

`t=0.66\ sec`

`\displaystyle Y=-((9.8)(0.66)^2)/(2)`

`Y=-2.134\ m`

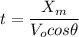
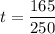
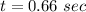
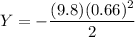
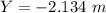
The bullet will hit 2.134 meters below the target

Note: In case the bullet is shot with the same angle as before, then the time will be

`\displaystyle t=(165)/(250cos0.539^o)=0.66\ sec`

`\displaystyle Y=250\ sin0.539^o\ 0.66-(9.8(0.66)^2)/(2)`

`Y=-0.582\ m`

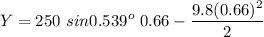
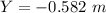
That small angle will result in a significant difference in height