Question

Look at the angles for all regular polygons. As the number of sides increases, do the measures of the angles increase or decrease? What pattern do you see

Answer 1

As the number of sides increases, the measures of the angles increase

see the explanation

Explanation:

we know that

The measure of the interior angle in a regular polygon is equal to

`x=((n-2))/(n)(180^o)`

where

n is the number of sides of the regular polygon

x is the measure of the interior angle in a regular polygon

we have that

Examples

A triangle

n=3 sides

`x=((3-2))/(3)(180^o)=60^o`

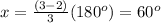
A square

n=4 sides

`x=((4-2))/(4)(180^o)=90^o`

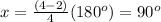
A pentagon

n=5 sides

`x=((5-2))/(5)(180^o)=108^o`

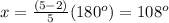
A hexagon

n=6 sides

`x=((6-2))/(6)(180^o)=120^o`

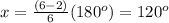
so

n ----> 3,4,5,6...

x ----> 60°,90°,108°,120°,...

As the number of sides increases, the measures of the angles increase

The pattern is
`x=((n-2))/(n)(180^o)`