Question

A textile fiber manufacturer is investigating a new drapery yarn, which the company claims has a mean thread elongation of 12 kilograms with a standard deviation of 0.5 kilograms. The company wishes to test the hypothesis LaTeX: H_0=\mu=12H0=μ=12 against LaTeX: H_1=\mu>12H1=μ>12 using a random sample of specimens. Calculate the P-value if the observed statistic is. Round your final answer to five decimal places

Answer 1

given,

mean = 12 Kg

standard deviation = 0.5 Kg

assume the observed statistic is = 11.1

now,
`\bar{X}=11.1 , \mu = 12 , \sigma = 0.5`

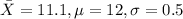
assuming the number of sample = 4

n = 4

Hypothesis test:

H₀ : μ≥ 12

Ha : μ < 12

now,

significant level α = 0.05

`z* = \frac{\bar{X}-\mu}{(\sigma)/(√(n))}`

`z* = (11.1-12)/((0.5)/(√(4)))`

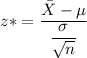
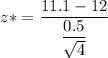
z* = -3.60

Test statistics, Z* = -3.60

P-value

P(Z<-3.60) = 0.002 (from z- table)

P- value = 0.002

now,

reject the value of H₀ when P-value < α

0.002 < 0.05

since, it is less P-value < α , we have to reject the null hypothesis