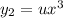Answer:
Explanation:
Given is a differntial equation
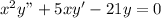 ,where x can take any positive value
,where x can take any positive value
One of the solution is
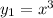
Let us assume the second solution
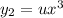
Differentiate this y2 two times and plug in the DE to reduce the order
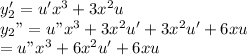
plug these in the DE

Put w=u'
xw'+11w=0