Question

Which expression correctly shows how to use the binomial theorem to determine the 4th term in the expansion of (2x^2y^3+y)^7 ?

Must be correct the highlighted is my answer I need to know if it's right or wrong.

Answer 1

Answer: Choice D) 560x^8y^15

========================================

Step-by-step explanation:

We dont involve sigma notation since we want just one term and we aren't adding up a bunch of things. It's really curious why your teacher is using sigma notation as it is incorrect. Everything else is fine.

-----------------

n = 7 is the outer most exponent of the binomial.

We have the terms for k = 0, k = 1, ... which means the 4th term is when k = 3.

n C k = (n!)/(k!*(n-k)!)

7 C 3 = (7!)/(3!*(7-3)!)

7 C 3 = (7!)/(3!4!)

So that explains the coefficient of (7!)/(3!4!). This is known as a binomial coefficient. Some books call the n C k function the "choose" function. Though other books call it a combination function. They're the same thing. Let's keep going to fully compute the binomial coefficient.

7 C 3 = (7!)/(3!4!)

7 C 3 = (7*6*5*4*3*2*1)/(3*2*1*4*3*2*1)

7 C 3 = (5040)/(6*24)

7 C 3 = (5040)/(144)

7 C 3 = 35

-----------------

a = 2x^2y^3

b = y

The kth term is in the form

(n C k)*(a)^(n-k)*(b)^k

Plug in the given values and simplify

(7 C 3)*(a)^(7-3)*(b)^3

35*(a)^4*(b)^3

35*(2x^2y^3)^4*(y)^3

35*16*(x^8y^12)*(y)^3

560*x^8y^12*y^3

560*x^8y^(12+3)

560x^8y^15

Answer 2

you need to rethink your selection

Step-by-step explanation:

None of the answer choices is correct. The fourth term does not need or have a summation symbol. (The effect of that symbol as written here is to multiply the term by 8.)

In (a+b)^7, the powers of "a" count down from 7 to 0. The fourth term has a^4b^3, so matches the left-side exponents of the first and last choices. Unfortunately, the right-side exponents of choice A don't match those on the left, so the only appropriate choice here is choice D.

As you know, the coefficient will be ...

C(7, 3)(2^4) = 35×16 = 560

The fourth term of the expansion is ...

560x^8·y^15

_____

When expressed with a summation symbol, the entire expansion (not just a single term) is ...

`\sum\limits_(k=0)^(7){\left((7!)/(k!(7-k)!)(2x^2y^3)^(7-k)y^k\right)}`

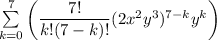
The fourth term has k=3.